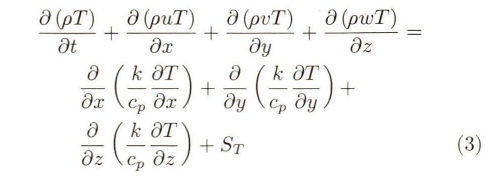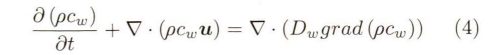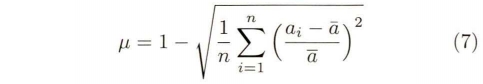摘要:氫氣作為全球脫碳目標的重要載體,輸送量是限制其大規模應用的主要瓶頸。摻氫天然氣是實現大流量輸送氫氣的一種重要途徑。氫氣的摻入導致流速畸變,降低超聲波流量計的性能。以摻入氫氣的甲烷為主要工質,對8種類型摻混管路內部的氣體流動狀態進行模擬仿真研究,分析流場內氣體速度和氫氣濃度的分布狀態;并對超聲波流量計的適應性進行分析,確定其推薦安裝位置。在超聲流量計的適應性分析中,三匝螺旋管時僅需15D;對于單螺旋結合變徑管的適應性影響更大,最小需要96D。通過比較,摻混管路C為最佳模型,摻混均勻時的氫氣摩爾分數約為3.9%。可為超聲波流量計在摻氫天然氣正確計量方面提供參考。
溫室氣體排放量增加導致全球極端天氣頻發,碳中和戰略轉型全球勢在必行叫。從《巴黎協定》無碳未來愿景及碳中和的全球目標網到我國碳達峰、碳中和的目標問,大規模氫氣輸送的綜合能源系統是實現這些目標的有效途徑。可再生能源大力發展及氫能技術與產業飛速發展為氫氣輸送和應用的快速發展提供了條件間。預計到2050年,全球可再生氫能能源達到將近10°kW,全球氫能市值將達到10萬億美元問。但氫能的生產地與使用地嚴重不匹配導致氫能的發展受限。相比傳統高壓瓶、低溫液化等物理儲運方式的小輸送量、高成本、長耗時7,管道輸送可實現長距離、大規模、低成本氫氣輸送且供氣量持續穩定。基于現有天然氣管網設施的優勢,將氫氣摻入天然氣管道輸送是解決氫氣運輸的必然發展趨勢閣。
氫氣的物理和化學性質與天然氣有較大差異。氫氣摻入天然氣改變管道內的氣體狀態引起溫度、壓力下降回,影響著輸送系統計量裝置的正確率。因此,對摻氫天然氣管道輸送過程進行監測及計量至關重要。超聲波氣體流量計具有壓損小、精度高、響應時間快和安全大等優點,在天然氣計量領域占據主導地1011。超聲波流量計針對混合氣體的計量需保證氣體混合均勻及管道內流速穩定對稱。
目前全球天然氣摻氫工業實踐項目共有39個,輸送量高達2900噸/年間。2004年,歐盟開始建設NaturalHy項目進行天然氣摻氫的應用研究,得到系統運行的最優摻氫比為20%則。2017年,英國能源供應公司開展“HyDeploy”天然氣摻氫項目,在第一階段工作證明利用現有天然氣管道加入20%氫氣摩爾分數是可行的5。2018年,國內首個天然氣摻氫示范項目研究呵,得到3%~20%之間的任意摻氫比。這些工業實踐項目為大規模天然氣摻氫進行管道輸送提供了正確的依據。由于摻氫天然氣屬于易燃易爆氣體,通常會先利用計算流體力學理論方法對摻氫天然氣的流場進行分析,并對超聲波流量計在管道中的適應性進行數值模擬。Chen等71對不同雷諾數下單右彎管和孔板下游的氫氣流動進行模擬分析。流量計位置越靠近擾動裝置,其誤差越大,增加聲路數量可有效減少誤差。Liu等18對管件連接處之后的天然氣流動進行仿真分析,并給出了超聲波流量計安裝要求。邵欣等l9對最常見的90°單彎頭圓管過渡區甲烷流場的流動機理進行分析。基于此安裝整流器可有效改善管道內流場速度分布,縮短超聲波流量計的安裝位置。唐曉宇等20對90°單彎管道內空氣流動狀態進行分析,隨下游直管距離增加,超聲波氣體流量計的計量偏差逐漸減小。當管道內流場分布非對稱時,會影響超聲波計量效果。擾動越劇烈,氣體摻混效果越好。國內外對于利用超聲波流量計進行摻氫天然氣計量的模擬仿真研究主要集中在改進聲道位置、數量、設置整流器、旋流器等,從而縮短超聲波流量計的安裝位置。缺少對管路結構進行改進,本文通過計算流體動力學(computationalfluiddynamics,CFD)仿真手段,研究摻氣天然氣管道結構為螺旋管(單螺旋、雙螺旋、三螺旋、六螺旋)和單螺旋+變徑管(膨脹管或收縮管)內的氣體混合規律及速度分布:并推薦了超聲波流量計在螺旋管路的安裝位置,為超聲波流量計的正確計量提供參考。
1摻氫天然氣管路模型
1.1數值仿真模型建立
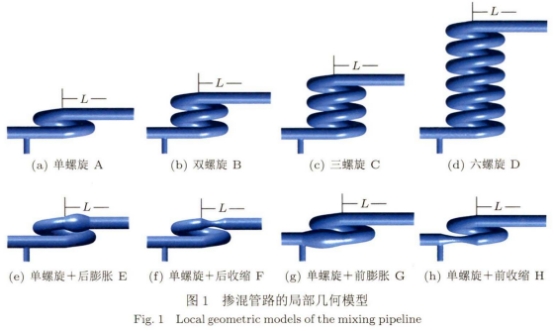
為研究管路結構對摻氫天然氣摻混狀態影響,本文在單螺旋管摻混管路的基礎上,使用Design.modeler構建了8種摻混管路的3維模型,如圖1所示。摻混管路分別為不同匝數螺旋管(單螺旋A型、雙螺旋B型、三螺旋C型、六螺旋D型)和單螺旋管路結合變徑管路(單螺旋+后膨脹E型、單螺旋+后收縮F型、單螺旋+前膨脹G型、單螺旋+前收縮H型)。由于將密度較輕氫氣從底部充入天然氣管路能取得較好的摻混效果,因此設計從管路底部充入天然氣。具體參數設置為:管路直徑D=100mm,甲烷入口直徑為1D,氫氣入口直徑為0.5D,出口直徑為1D,螺旋管曲率半徑為2D。氫氣入口(支管軸線)距螺旋管起始截面長度為3D,多匝螺旋管螺距為1.5D。膨脹管長度為3D,膨脹管直徑最大處為.1.5D;收縮管長度為3D,收縮管直徑最小處為0.5D。為使氣體充分摻混,將下游管路總長度設置為150D。在計算不同匝數螺旋管及單螺旋管路結合變徑管路結果時,定義的長度L是以螺旋.管終止截面為起點。
1.2數學模型
氣體流動需滿足連續性方程、動量守恒方程、能量守恒方程等基本控制方程。
天然氣和氫氣在摻混過程及在管道流動中的連續性方程為

式中,p為流體微元體上的壓力;u為速度矢量;Fx,和Fy為微元體在x軸,y軸和z軸方向上的力;Txx,Tyx,Tzx,Txy,Tyy,,Tzy:,Txz,Tyz,Tzz為微元體表面的不同黏性應力分量。
摻混過程及在管道流動中的能量守恒定律為
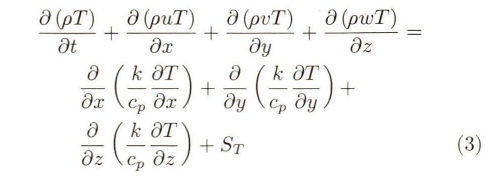
式中,k為流體傳熱系數,Cp為比熱容,T為溫度,St為流體內熱源和因黏性作用流體機械能轉化為熱能部分。
天然氣與氫氣摻混時需開啟組分運輸,此時管路中氣體的傳播規律
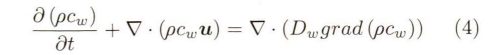
其中,ρCw為組分w的質量濃度,Dw為組分w擴散系數。
天然氣摻氫的過程中遵循理想氣體狀態方程。
由于摻混過程中的氣體參數(流量、壓力等)發生變化,會導致摻混氣體的密度、動力黏度、狀態方程參數等產生變化。具體表達式

其中,Pop為摻混氣體的工作壓力,p為相對于Pop的局部相對壓力,R為氣體常數,T為氣體溫度,Yi為第i種氣體的質量分數,Mɷi為第i種氣體.的分子質量。

其中,Um為摻混氣體動力黏度,M為氣體種類數,出為第i種氣體的摩爾百分比,ui為第i種氣體的動力黏度,Mi為第i種氣體的相對分子質量
本文以摻混均勻度u和速度變異系數(coffi-cientofvariation,COV)來評價混合程度,輸出不同數據采集線處氫氣濃度以及速度。
摻混均勻度μ計算公式為
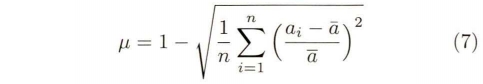
其中,`a為監測點氫氣濃度測量值的平均值,n為取樣截面內所設監測點總數,a;為第i個監測點所得的氫氣濃度值。各截面內設置23個監測點進行摻混均勻度μ的統計計算。
速度COV計算公式為

其中,σ為標準偏差,`c為監測點測量值的平均值,ci為第i個監測點所得的氣體速度值。各截面內設置23個監測點進行速度COV的統計計算。
1.3網格劃分
本文利用ANSYSWorkbench中的Mesh模塊,選用四邊形或三角形網格法對流體域進行網.格劃分。網格數量對Fluent仿真計算結果有至關重要的影響。理論.上所采用的特征尺寸網格越小,得到的仿真結果越正確。但隨著網格數量的增加,對計算硬件資源的要求更高,而且導致計算時間延長,降低求解結果的收斂性。本文以摻混管路A,E為代表,分析稀疏、中等、稠密三種網格特點對出口氫氣濃度變化的影響,進行網格無關性驗證。結果如表1所示,隨網格數量增加,不同網格特點出口處氫氣摩爾分數波動很小。綜合網格平均偏斜系數和網格平均質量系數分析,三種網格特點下的網格質量均滿足模型需求,可以忽略網格對仿真計算結果精度的影響。
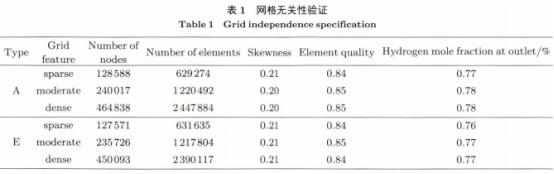
基于上述無關性分析,本文選用中等特點的網格。網格尺寸為10mm,單元數為1220492個,節點數為240017個。最終網格平均偏斜系數為0.20,標準偏差為0.11。偏斜系數在0~1范圍內,越接近0網格質量越優秀。網格平均質量系數為0.85,標準偏差為0.09。質量系數在0~1范圍內,越接近1網格質量越高,網格質量滿足模型需求。
1.4邊界條件設定
湍流模型選用最具有適用性的標準k-ε模型,適用氣體摻混計算,在減小計算量的同時保證了計算精度。在操作條件中設定溫度為300K,重力沿y軸負方向為9.8m/s2。管道入口均設置為速度進口邊界條件,主管道入口速度為6.75m/s(流量:190.8m3/h),摻混管道入口速度為3m/s(流量:21.2m3/h);主管道和摻混管路入口初始湍流參數一致,湍流強度為5%,湍流黏度比為10。管道出口設置為壓力出口邊界條件,出口回流湍流強度為5%,回流湍流黏度比為10。水力直徑為0.1m。主管道入口氣體為純甲烷,摻混管路入口氣體為純氫氣。將初始內部工質設為100%甲烷后進行混合初始化,最后利用SIMPLEC算法進行計算求解。
2結果與分析
2.1不同匝數螺旋管的氣體流動分析
在工程實踐過程中對氣體的摻混效果進行評價時,一般認定當摻混均勻度μ≥95%時,氣體在微觀.上已達到摻混均勻叫。如Kong等網以摻混均勻度μ是否≥95%,來判定現有天然氣管道中摻入氫氣是否摻混均勻。氣體在傳輸擴散過程中會改變氣體組分的濃度分布,同時影響氣體流速分布。甲烷和氫氣流經螺旋管摻混管路時,會受到強烈二次流以及高濃度差的影響,加速氣體擴散,管路中的氣體最終向摻混均勻的方向發展。如圖2所示為摻混管路(A,B,C,D)內氣體摻混均勻度與螺旋管出口截面位置的關系。螺旋管管路的氣體混合均勻性均隨著管路匝數和摻混距離的增加呈現.上升趨勢。螺旋管路的匝數越多,摻混均勻所需的摻混距離越短。摻混管路A和B分別在146D和69D時實現氣體摻混均勻。而當選用匝數為3圈的摻混管路C時,在螺旋管出口3D的距離,摻混均勻度已經達到摻混均勻的要求。由此可知,增加螺旋管的匝數可以非常有效地縮短摻混距離,摻混管路C的效果已經非常好。若再增加匝數到六螺旋(摻混管路D)已無實際意義,反而會導致摻混均勻時的距離增加到15D。
news-images/news-2036_wps
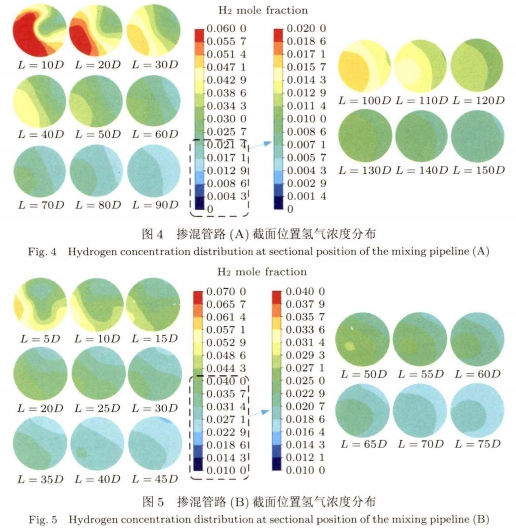
為了更清晰明了地觀察天然氣摻氫混摻管路(A,B,C,D)的摻混過程,以四種摻混管路的螺旋管出口為起始點,每隔1D設置一個監測截面。本文得到數據均是瞬態仿真的結果,在初始時刻氫氣摩爾分數為0,表示氫氣還沒擴散至指定位置。如圖3所示摻混裝置C為最佳摻混模型,在15D截面處,氫氣摩爾分數隨注入時間,由0到9.8%的變化過程。氫氣流動擴散1.03s后,初次達到摻混均勻時,在15D截面處瞬時氫氣摩爾分數為3.9%。天然氣摻氫混摻管路A,B,C,D分別經過3.92s,2.19s,1.50s,2.03s后,氫氣的濃度等于進口氫氣與甲烷的流量比(仿真結果是取到9.8%),表示氫氣已擴散至指定位置,并達到穩態。圖4~圖7是天然氣摻氫混摻管路A、B、C、D分別在2.11s(146D截面處)、1.40s(69D截面處)、1.03s(15D截面處)、1.37s(15D截面處)時刻,摻混管路在不同距離截面處的氫氣摩爾分數云圖,與穩態時的摩爾分數不同。
news-images/news-2036_wps
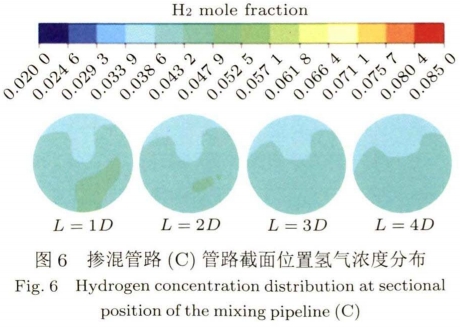
如圖4所示摻混管路A在螺旋管路出口處渦流作用非常劇烈,其分層現象明顯。且不同于--般氫氣的上下分層,摻混管路A中管道中的氫氣直存在左右分層,直至摻混距離在140D~150D達到摻混均勻,此時氫氣摩爾分數均約為0.8%。圖5所示摻混管路B的管路截面氫氣濃度分布變化規律與圖4相似,直至摻混距離在65D~70D達到摻混均勻,氫氣基本不再分層,此時氫氣摩爾分數均約為1.9%。而圖6所示的摻混管路C在螺旋管道出口處就已經基本達到摻混.均勻,氫氣已基本不存在分層,此時氫氣摩爾分數均約為3.9%。相比摻混管路C的三匝螺旋管,圖7所示摻混管路D增加到六匝螺旋的摻混效果反而下降。螺旋管道出口氫氣分層,直至摻混15D時達到摻混均勻,氫氣不再分層,此時氫氣摩爾分數約為2.0%。
氣體摻混后速度分布云圖,如圖8所示,速度變化受匝數影響較小。摻混管路A和B均約在15D之后,摻混管路C約在10D之后,速度等高線變得非常規則,越來越趨近于圓形,而摻混管路D約在40D后能達到同樣效果。此時這四種類型摻混管路內的氣體速度已達到充分穩流發展的狀態,之后基本不再發生變化。流速分布很.合理,距離管道中心線越近其速度越快,符合黏性定律。


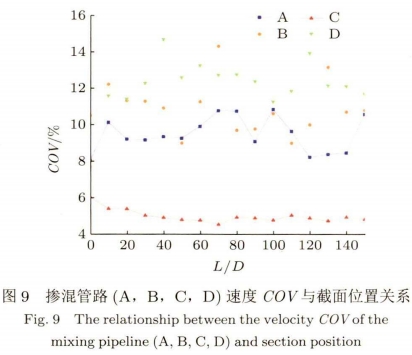
摻混管路(A,B,C,D)速度COV與截面位置的關系如圖9所示。隨著截面位置向下游移動,摻混管路(A,B,D)的速度COV一直處于波動狀態,但皆不超過15%。相比于A,B和D,摻混管路C內氣體速度分布更為均勻,其速度COV-直穩定在5%左右。綜合考慮氣體摻混均勻度μ和速度COV,摻混管路C為最佳摻混模型。
2.2單螺旋結合變徑管的氣體流動分析
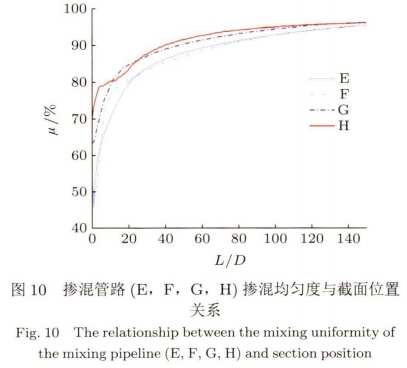
如圖10所示為摻混管路(E,F,G,H)的管路內氣體摻混均勻度與截面位置關系,摻混管路E,F,G,H是在單螺旋的基礎上添加變徑管(膨脹管或收縮管),分別在136D,132D,107D,96D處時實現氣體摻混均勻。相比單螺旋管的146D,在不同位置添加任何變徑管均能在.不同程度.上實現縮短摻混距離的效果。將變徑管置于單螺旋管之前氣體初步摻混后再進入單螺旋管進一步摻混,明顯比置于單螺旋管之后更能有效地縮短摻混。而氣體進入收縮管內流動速度會增大,此時的擾動更加劇烈,有助于氣體摻混。針對變徑管位置及類型,摻混管路H(即前收縮.管)的摻混效果更好。
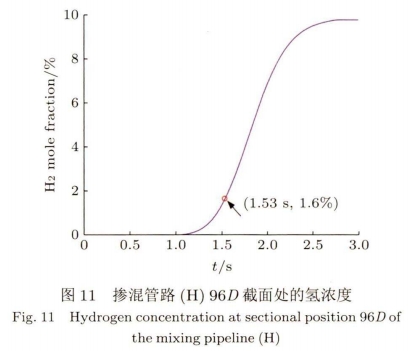
本組所得數據是瞬態仿真的結果,在初始時
刻氫氣摩爾分數為0,表示氫氣還沒擴散至指定位置。如圖11摻混裝置H為最佳摻混模型,在96D截面處,氫氣摩爾分數隨注入時間,由0到9.8%的變化過程。氫氣流動擴散1.53s后,初次達到摻混均勻時,在96D截面處瞬時氫氣摩爾分數為1.6%。天然氣摻氫混摻管路E,F,G,H
分別經過3.06s,2.95s,2.94s,2.48s后,氫氣的濃度等于進口氫氣與甲烷的流量比(仿真結果是取到9.5%),表示氫氣已擴散至指定位置,并達到穩態。圖12~圖15是天然氣摻氫混摻管路E,F,G,H分別在1.91s、1.89s、1.69s、1.53s時刻,摻混管路在不同距離截面處的氫氣摩爾分數云圖,與穩態時的摩爾分數不同。.

對比圖12~圖15,四種類型摻混管路的管道截面氫氣濃度變化規律很相似。在螺旋管道出口.處氫氣均存在明顯的左右分層現象。但隨著距離的增加,最終均能達到摻混均勻,氫氣基本不再有分層的狀態。但不同類型管道達到此狀態所需的距離不一。如圖12所示摻混管路E需約130D~140D的距離才能達到此狀態,此時氫氣摩爾分數約為0.9%;圖13所示的摻混管路F同樣需約130D~140D的距離達到此狀態,此時氫氣摩爾分數比摻混管路E略大,約為1%;圖14所示的摻混管路G需約100D~110D的距離達到此狀態,此時氫氣摩爾分數約為1.2%;圖15所示的摻混管路H需約90D~100D的距離達到此狀態,此時氫氣摩爾分數約為1.6%。
氣體摻混后速度分布云圖如圖16所示。管道尺寸的變化會導致內部的氣體流動速度突變,使得氣體速度穩定下來所需的距離更遠。摻混管路E,F,G,H均在約30D之后,速度等高線形狀穩定下來,比單螺旋管(15D)的截面距離大一倍。

摻混管路(E,F,G,H)速度COV與截面位置的關系如圖17所示。初始截面位置時,摻混管路(E,H)的速度COV最大,約為17%。而隨著截面位置向管道的下游移動,這四種類型的摻混管路的速度COV均穩定在8%附近。雖然四種類型的摻混管路最終穩定時的COV差別很小,但相比摻混管路(E,F,G),摻混管路(H)的速度COV達到穩定時所需的距離最短,僅需10D。故摻混管路H為最佳摻混模型。

本文設置為10%的摻混比,穩態仿真的時候,組分濃度只是依賴于進口流量比。但在瞬態仿真的時候,組分濃度不僅依賴于進口流量比,還跟流體的運動時間、狀態有關。瞬態計算中,發展階段變化屬于介質置換過程(初始管內全部甲烷),詳細討論各摻混管路的氫氣濃度演化的過程。而達到穩定后,沿程的變化特征反映的是氫氣和甲烷分層及其滑移效果,氫氣密度小,相同截面間壓差會有更大的流動速度,摩爾濃度小于進口流量直接計算值。通過對比在相同截面位置的摻混管路A氫濃度(圖4)對應速度(圖8)以及摻混管路E的氫濃度(圖12)對應速度(圖16)分析可得:只有當二者摻混均勻后,氣體組分間相互作用,均質、同速運動,進口流量直接計算的摩爾濃度才與實際相符。計算結果氫氣摩爾濃度偏低9.8%(入口設置的10%),正反映了非均勻摻混狀態,甚至明顯分層結構下,氫氣流速高過甲烷,存在明顯介質間滑移現象這個事實。也進一步證明摻混效果對真實速度正確和正確測量的必要性。
2.3適應性條件
只有當混合氣體摻混均勻,且管道內氣體流速已達到充分穩流的對稱分布狀態時,才能保證超聲波流量計計量的正確率。因此,本文結合不同結構的摻混管路仿真模擬結果,保證超聲流量計計量正確率的推薦安裝位置如表2所示。由表2可知螺旋管的匝數以及變徑管位置對流量計安裝距離的影響最大。
news-images/news-2036_wps
3結論
為研究不同天然氣摻氫管路結構對超聲波流量計安裝距離的影響,本文針對不同匝數螺旋管路、單螺旋結合變徑管路進行CFD仿真模擬,得到氫氣摩爾分數云圖以及反映其摻混均勻度的μ和COV的變化規律,最終得到最佳摻混模型及超聲波流量計安裝距離。具體內容如下。
(1)對于不同匝數螺旋管的氣體流動分析,在0~20D間μ的變化最為劇烈,即此時氣體擾動最為劇烈,氣體摻混主要在這一范圍進行。一般螺旋的匝數越多,超聲流量計安裝距離越短。當增加到三螺旋時僅需15D。此后再增加匝數已無實際意義,增加到六螺旋時的超聲流量計安裝距離仍為15D。.
(2)對于單螺旋結合變徑管的氣體流動分析,在0~25D間μ的變化最為劇烈,此范圍氣體摻混效率更好。相比變徑管的類型,其安裝位置明顯對超聲流量計安裝距離影響更大。同樣的膨脹管安裝在前端(107D)比后端(136D)所需的距離少19D,同樣的收縮管安裝在前端(96D)比后端(136D)所需的距離少26D。而同樣位置的不同類型變徑管,其超聲流量計安裝距離差異性較小。
(3)不同匝數螺旋管下,摻混裝置C為最佳摻混模型,氫氣流動擴散初次達到摻混均勻度μ時,在15D截面處瞬時氫氣摩爾分數為3.9%;單螺旋管結合變徑管下,摻混管路H為最佳摻混模型,氫氣流動擴散初次達到摻混均勻度μ時,在96D截面處瞬時氫氣摩爾分數為1.6%。
本文來源于網絡,如有侵權聯系即刪除!