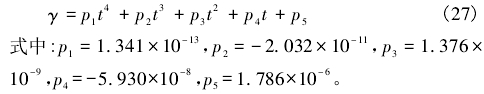摘要:流量測量是影響水輪機效率測試精度最主要的因素。大管徑流量測量的方法主要采用超聲波法,然而,其測量精度及誤差構成尚無有效的校驗方法。結合時差法超聲波流量計的測流原理,推導得到流量綜合誤差,建立測流誤差描述模型。提出一種基于流量測量理想系統(tǒng)來進行誤差分析的量化方法,為超聲波測流系統(tǒng)的誤差分析與控制提供一種新的途徑。通過測流.理想系統(tǒng)對超聲波測流精度的影響因素進行仿真研究,分析了各項參數(shù)測量誤差對系統(tǒng)綜合誤差的影響,針對影響較大的主導因素提出了相關修正方法,并對系統(tǒng)綜合誤差的控制進行了分析。最后搭建實驗系統(tǒng)進行研究,實驗結果初步驗證了該方法的有效性。
0引言
水輪機效率是水電站經濟運行的基礎數(shù)據(jù)。國際電工委員會推薦的熱力學法“在國內魯布革電站進行過嘗.試四,其實施難度較大。影響水輪機效率測試精度的主要因素是流量測量,特別是大管徑流量測量。目前,大管徑流量測量的方法主要是超聲波法,測量原理應用最多的是時差法時差法測流原理簡學直觀,但要提高測流精度涉及因素較復雜7-四,而且實驗所得數(shù)據(jù)本身就存在誤差,測流誤差的校驗尚無簡單有效的方法,因此研究相關因素的影響并有針對地進行優(yōu)化和控制對提高測量精度十分必要。
目前,對測流精度影響因素已基本取得共識。超聲波測:流誤差的原因主要有3個方面:1)斷面流速均勻計算造成的誤差;2)超聲波傳感器安裝和測量精度造成的誤差(聲音傳播信號是否能被傳感器正確收到,聲路長度和聲路角的測量誤差);3)環(huán)境及介質對超聲波流量計時間計算造成的誤差。目前的研究基本.上都是圍繞這3個方面展開的。分析了影響測量精度的因素,對溫度、流速和管道內置反射片所造成的測量誤差進行了分析,提出了具體的誤差修正補償方法,但其反射片安裝在流體內部,對流場可能有影響且不便測量操作;楊志勇等中在推導流量計算公式的基礎上得出影響測量結果的主要因素,有針對性的提出了延長聲波法、溫度補償法、流量修正法、系統(tǒng)集成化設計,但其重點在信號處理上且針對小管徑進行分析;楊聲將等對噪聲、臟污、壓力及溫度測量對超聲波流量計計量系統(tǒng)性能的主要影響因素以及控制對策進行了分析探討,但實驗現(xiàn)場仍不能滿足相關要求,造成儀器測量的不正確性;耿存杰等以主要介紹了利用實驗室現(xiàn)有的液體流量標準裝置,對超聲波流量計在不同管道材質、不同管徑的條件下進行流量系數(shù)的修正,但條件變化時需重新進行標定,不便于使用。
本文討論了造成超聲波流量計測流誤差的影響因素,推導得到流量綜合誤差,提出一種基于流量測量理想系統(tǒng)進行誤差分析的量化方法,分析了單個因素對流量相對誤差的影響程度,針對主導因素給出了相應的修正方法,最后對綜合誤差的控制進行了分析,為流量的修正提出了新思路。
1時差法超聲波流量計工作原理
超聲波流量計測量系統(tǒng)最常用的測流原理是“時差法”。超聲波換能器采用的是管外“Z"型安裝方式,測量原理如圖1所示。探頭1發(fā)射信號,信號穿過管壁1、流體、管璧2后被另一側的探頭2接收到;在探頭1發(fā)射信號的同時探頭2也發(fā)出同樣的信號,經過管壁2、流體、管壁1后被探頭1接收到;由于流體流速的影響超聲波在順流和逆流情況下的傳輸時間t1和t2不同,因此根據(jù)時間差便可求得流速,進而得到流量值。

如圖1所示,記管道內徑為D.超聲波在水中聲速為c,超聲波傳播線路上的流體流速為v,聲路角為θ,超聲波在換能器和管壁中的總傳播時間7τ0,則順流、逆流傳播時,超聲波傳輸時間為:

時差式超聲波流量計測量通常采用的是超聲波傳播路徑上流體的線平均流速,而實際管道橫截面上的流速分布是呈拋物線形態(tài)的,這就造成了斷面流速計算造成的誤差,具體如圖2所示。

由圖2可知,流體線平均流速0與截面平均流速VD存在以下關系:
大管徑超聲波流量計的現(xiàn)場校驗試驗比較困難,其流量測量本身就存在一-定誤差,采用試驗驗證方法是沒有意義的。本文提出一種基于理想系統(tǒng)的驗證方法,即按超聲波測流的布置形式.給出理想條件下的參數(shù)值,假設存在參數(shù)測量誤差,按上述公式進行計算,得到各項參數(shù)對流量測量誤差的影響程度.進而分析得到影響流量測量誤差的主導因素,再進行誤差修正。
設置一個理想系統(tǒng):被測流體為清水,管道內徑為D=3.00m,超聲波流量計安裝角為θ=40°,水體溫度t=20℃,超聲波傳播速度為c=1485.00m/s,流體截面平均流速vD=4.00m/s.流量為Q=28.26m3/s。理想條件下時間測量儀器精度完全達到要求時得到的時間差為△t=1.30x10-5s。
2單因素誤差分析
由式(6)知流量與管道內經D、聲路角θ、超聲波在水中的速度c、及流量系數(shù)K有關,因此流量測量中重點考慮這4項因素。
根據(jù)間接測量的誤差理論,對式(6)做變換可得流量的絕對誤差σQ,為:

將式(6)代入式(7),可得:
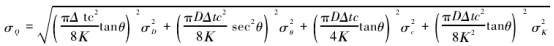
式中:σx表示變量{D,θ,c,K}的絕對誤差。
在超聲波流量計安裝完成后,取理想條件所對應的各參數(shù)值為基值。將式(8)兩邊同時除以Q,化簡整理后得相對誤差為:

管徑測量精度一般能達到0.1%,按相關倍數(shù)取值得到不同管徑誤差σ0D時的流量誤差如表1所示。
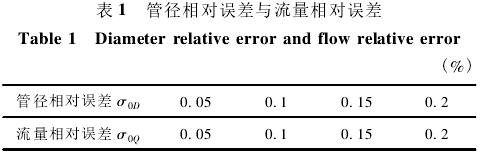
由式(10)可知,管徑的相對誤差會造成1倍的流量相對誤差,由此可見理論.上管徑誤差對流量誤差有著較大的影響。在實際工程應用中,大管徑的測量誤差較小,例如,管徑為3.0m,測量誤差為±0.05%時,誤差絕對值為±1.5mm,而實際測量時,誤差絕對值遠小于±1.5mm。對照表1可知,管徑測量誤差造成的流量誤差能控制在遠小于±0.1%以內,并且鋼管結垢現(xiàn)象也不太明顯,因此管道測量精度的影響可以先忽略。
2.2聲路角誤差
由式(6)可知,當聲路角測量存在誤差σθ時,流量相對誤差為:

分別取不同聲路角θ和聲路角誤差σθ,得到的流量相對誤差如表2所示。

聲路角為40°時,0.5°的聲路角誤差造成的流量相對誤差能達到1.78%左右的,1°的誤差造成的流量誤差高達3.6%,隨著聲路角誤差的增大流量相對誤差增長也較為明顯。同--聲路角誤差下θ=30°和θ=60°時的流量相對誤差相近,與兩者相比θ=40°時的誤差較小,因此,初步推斷存在一個最佳聲路角使得流量相對誤差最小。
2.3聲速誤差
聲速會隨溫度變化而變化,根據(jù)威拉德研究給出的水聲速與溫度關系式”得到標準大氣壓下水中聲速與溫度的關系式可寫為:

在20℃時超聲波傳播速度為c=1485m/s.當水溫發(fā)生變化,t=0℃時,c=1422.838m/s,t=40℃時,c=1528.678m/s,對應的流量相對誤差分別為8.266%、5.889%。
如若忽略溫度的變化,由上兩式知20C的變化量下流量相對誤差平均能達到7%左右。并且根據(jù)該方式計算得到在0~40℃范圍內超聲波傳播速度差值可達105.84m/s,對應流量測量誤差為14.155%。因此根據(jù)相關關系式來進行聲速調控很有必要。
在該理想系統(tǒng)“下,取不同聲速誤差,代入式(13)可得流量相對誤差如表3所示。
由表3可知.1%的聲速誤差會造成2%的流量誤差,但同一時段的溫度變化并不明顯,其誤差很小可以控制在0.01%范圍內,其波動可以通過與敏感的溫度傳感器相結合的方法將溫度變化引起的聲速改變及時傳遞給流量計,以此來減小誤差。

2.4流量系數(shù)K造成的誤差
流場流態(tài)對流量測量有一定的影響,其影響主要是通過其流速系數(shù)K來體現(xiàn)。
管道內的流體實際流速分布規(guī)律為:

由上述分析知,修正系數(shù)K與雷諾數(shù)Re的大小有著直接關系,并且其變化范圍較廣取值很難確定,因此根據(jù)外界因素不同得出兩者關系對流量的正確測量有很重要的影響。
綜上所述,對流量測量影響較大的因素為聲路角θ和修正系數(shù)K。
3主導因素修正
3.1聲路角誤差修正
由于直接測量角度較為困難,且其測量儀器精度不能達到要求,因此考慮在測量方式上進行優(yōu)化,提出一種依據(jù)長度安裝要求達到控制聲路角的方法。

圖4所示為流量相對誤差與聲路角的關系。由圖4可知,在聲路角測量誤差較小時,流量測量相對誤差隨聲路角(安裝角)大小的變化不明顯,如圖中紅線(σθ=0.1%)所示。反之,若聲路角測量誤差較大,則流量相對誤差隨聲路角的變化呈拋物線變化,如圖中綠線(σθ=1°)所示,且存在一個最小值。聲路角不變時,流量相對誤差會隨著絕對誤差的增大而增大。
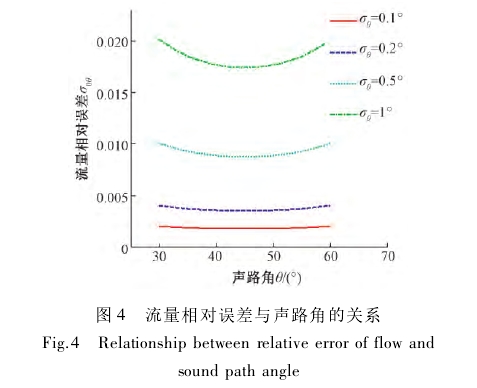
令შσ/შθ=0,有θ=45°時,流量的相對誤差σ0Q取最小。
3.2K值的修正
K系數(shù)與流體型態(tài)有關且隨雷諾數(shù)變化而變化,研究不同型態(tài)下的K系數(shù)隨雷諾數(shù)變化規(guī)律有利于流量補償計算和提高測量精度。
由式(24)可知,層流時的修正系數(shù)K=4/3,但對大管徑來說,場內流態(tài)一般是紊流情況。因此,本文重點分析紊流時的流量系數(shù)K的修正。
紊流時修正系數(shù)與雷諾數(shù)有關,經驗公式為:
K=1.119-0.011xlgRe(25)
依據(jù)式(25)可知.流量系數(shù)與雷諾數(shù)呈線性關系,雷諾數(shù)變化直接影響流量系數(shù)的取值。本文考慮根據(jù)雷諾數(shù)相關的變量來對K值進行修正。雷諾數(shù)計算公式為:

式中:V為平均流速;D為管道內經;Ƴ為流體運動粘度。
由式(26)可知,雷諾數(shù)大小與3個變量有關。當管徑一定時,雷諾數(shù)會隨著平均流速和流體粘度變化而變化。水的粘度隨溫度的變化而變化,溫度變化會影響到雷諾數(shù),進而影響流量修正系數(shù)K的值。因此找出粘度隨溫度的變化關系對K的正確性有著一定的影響。
流體粘度受流體溫度的影響具有非線性特點,通過擬合溫度與運動粘度值,得到不同溫度下水的運動粘度的曲線,如圖5所示。
多項式擬合表達式為:
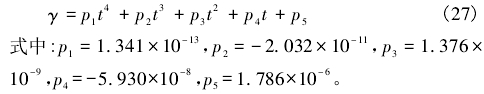
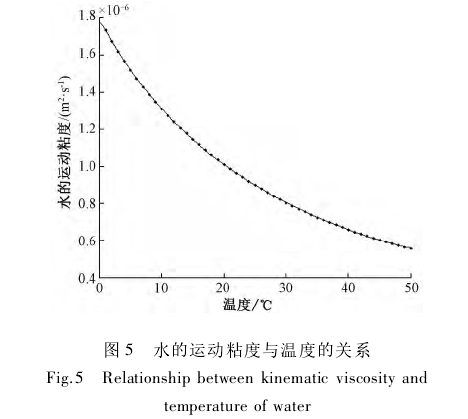
隨著溫度的升高,水的粘度非線性特征愈發(fā)明顯。在0~50℃范圍內水的粘度值差值可達到1.2x10-6m2/s,對應的雷諾數(shù)誤差為66.67%,不容忽視。
將得到的擬合曲線依次代入式(19)、(20)得:
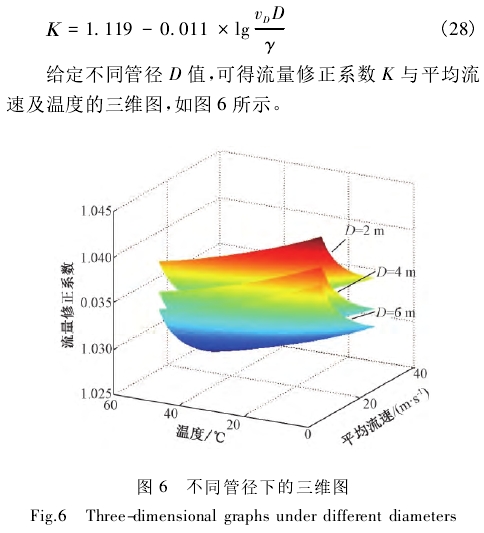
由圖6可以看出,同一管徑條件下,流量系數(shù)隨平均流速和溫度的增加都呈非線性減小趨勢。其他條件一定時,隨著管徑D的增大流量系數(shù)K值會減小。
此修正方法將溫度和流速變化與K值聯(lián)系起來,兩者任一值發(fā)生變化都能找到相對應的修正系數(shù)值,為準.確測得流量提供了一定的理論基礎。
4系統(tǒng)誤差控制
根據(jù)式(9)知流量相對誤差由內徑D、聲路角0、聲速c及流量系數(shù)K值組成,因此系統(tǒng)的誤差控制需要對這4個因素進行綜合考慮。
若原設理想系統(tǒng)中的流量測量誤差精度要控制在±0.5%以內,即σoQ<0.5%。由綜合誤差式(9)知,各因素至少要滿足σ0x<0.5%。
1)內徑誤差
目前的一-些管徑測量儀器已經能達到較高的精度,像激光掃描測徑儀精度最高可達0.5μm,其誤差可控制在0.005%以內甚至更小,完全滿足單因素精度要求。由于管徑在制造過程中可能存在一定的誤差,因此在對管徑進行測量時可在安裝位置處采用多處多次測量求平均值的方法來盡可能減小此部分誤差。
2)聲路角誤差
聲路角測量較難進行,將角度測量轉化成距離測量后,在安裝時按照需要角度進行計算后再安裝便能減小其誤差,其誤差可以控制在0.05%以內,也滿足單因素的誤差要求。.
3)聲速誤差
同一時段內的溫度變化很小,因此其造成的聲速變化不明顯,根據(jù).上述聲速溫度修正公式進行修正后,其誤差便可控制在0.1%以內,滿足單因素的精度要求。
由于管徑測量精度很高,在此忽略此項誤差。將θ=45°,σ0θ=0.05%,σ0C=0.1%代入式(9)得:

由上式得至少要滿足σ0K<0.45%系統(tǒng)才能達到要求。若想進一步減小綜合誤差,則需優(yōu)化各因素測量儀器,使其誤差控制在更小范圍內。
根據(jù)上述分析,超聲波測流精度控制中,最困難的因素就是管道流速形態(tài)的處理,即本文中提到的系數(shù)K。如何進--步提高管道流速分布對測量的影響及得到其修正方法,尚需開展進一步研究。
5實驗系統(tǒng)搭建
對于大管徑超聲波流量計測流的驗證性實驗是比較困難的。利用水機電耦合真機實驗室,在引水管直管段上搭建實驗平臺來進行了相關實驗,對本文提出的影響測量精度幾方面的因素進行了試驗分析。
試驗條件:安裝點選取位置前后直管段距離均滿足安裝要求,直管段外徑D=616mm,管壁厚度δ=8mm.實驗環(huán)境溫度15℃,流量測量儀器采用的是康創(chuàng)TY1010PW單聲道便攜式超聲波流量計,其精度為1%。實驗裝備如圖7所示。
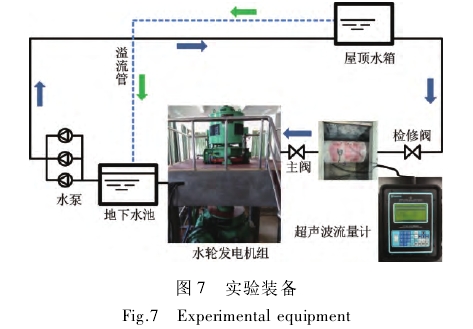
通過效率試驗測得相關數(shù)據(jù),在實驗中改變出力P來測流量Q,并根據(jù)上述分析得到了流量系數(shù)K值,數(shù)據(jù)如表5所示,水輪機功率與流量的關系如圖8所示。

由圖8可以看出,水輪機功率與流量的關系與廠家給出的流量特性是一致的。本實驗各項誤差控為σD=0.005%,σθ=0.05%,σc=0.1%。從綜合誤差分析來看,當流量系數(shù)K值滿足σoK<0.45%時系統(tǒng)誤差便可控制在0.5%以內。
由表5可以看出。流量變化從0.176~0.5m/s時,流量系數(shù)K值從1.0585~1.0535,變化范圍較小。取功率P=55kW時.測得的流量Q=0.5m3/s,考慮其精度1%,則實際流量范圍為0.495~0.505m3/s,從表可以看出,流量系數(shù)K值的變化波動值約為0.0005,精度可達到0.05%,其誤差范圍完全滿足綜合誤差控制要求,因此,初步推斷該方法有效。
6結論
本文提出了一種基于理想測流系統(tǒng)的超聲波流量計誤差分析方法,討論了造成超聲波流量計測流誤差的原因、誤差產生影響因素。通過量化方法對各影響因素進行討論,針對主導因素給出了相關的誤差修正方法,對綜合誤差控制進行分析并開展了試驗進行驗證。從實驗結果可初步推斷該方法是有效的。基于理想測流系統(tǒng)分析方法弄清了各參數(shù)的影響程度,對于現(xiàn)場安裝和進行實測試驗都有一定的指導作用,為后期超聲波流量計的誤差修正提供了新思路。該方法在優(yōu)化水輪機效率計算精度的同時也為超聲波流量計的設計提供了參考。
本文來源于網(wǎng)絡,如有侵權聯(lián)系即刪除!